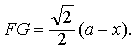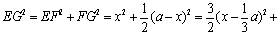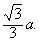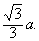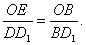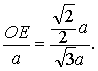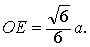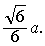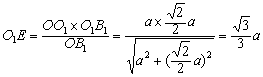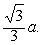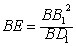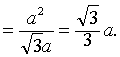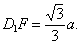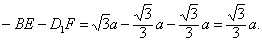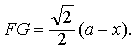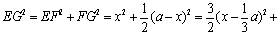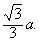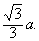两条异面直线的距离liangtiao yimian zhixian de juli

两条异面直线的公垂线在这两条异面直线间的线段的长度.
两条异面直线的距离是两条异面直线之间的“远近”的量度.
求两条异面直线的距离常用的方法是：
❶根据定义，找出（或作出）两条异面直线的公垂线，并求出公垂线在两条异面直线间的线段的长度.如下面例题中的第❶小题.

❷利用“如果一个平面通过两条异面直线中的一条且平行于另一条，那么后一直线与平面之间的距离等于两条异面直线的距离”(参见“两条异面直线的公垂线”).如下面例题中的第
❷小题的解法1.

❸利用“如果两个平行平面分别通过两条异面直线，那么这两个平行平面间的距离等于这两条异面直线的距离”.如下面例题中的第
❷小题的解法2.

❹利用代数中求函数的极值的方法.如下面例题中第
❷小题的解法3.

❺利用公式(参见“异面直线距离的计算公式”).
例 正方体ABCD-A₁B₁C₁D₁的棱长为a.
❶求AC与BD₁间的距离.

❷求A₁C₁与B₁C间的距离.

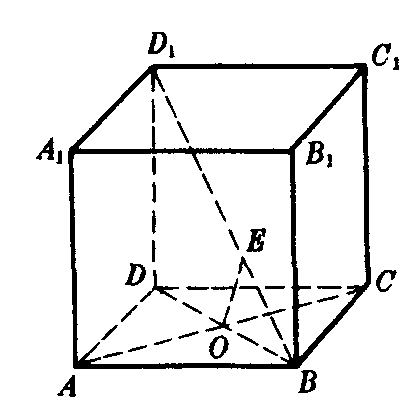
图1

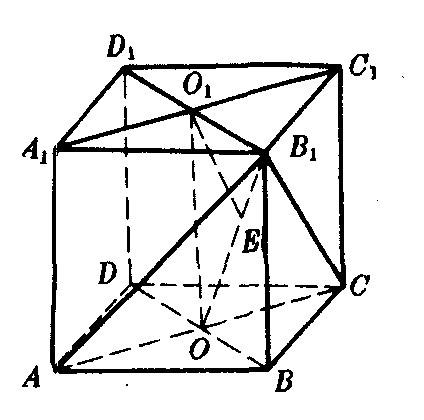
图2

解 ❶如图1，连结BD.设AC∩BD=O.因为DD₁⊥平面AC，所以DD₁⊥AC.又AC⊥BD.所以AC⊥平面BDD₁.在平面BD_D1中，过O作OE⊥BD₁于E.则OE是AC和BD₁的公垂线.因为Rt△BEO∽Rt△BDD₁，所

以

即

所以

因此

AC与BD1间的距离为

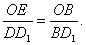
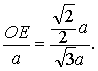
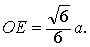
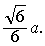
❷解法1 如图2，连结AC,BD,B1D₁,A_B1.设AC∩BD=O,A₁C₁∩B₁D₁＝O1.易证A₁C₁∥平面AB₁C.因此A₁C₁上任何一点到平面AB₁C的距离就是A₁C₁与B₁C间的距离.因为∠O₁B₁C=∠O₁B₁A.容易证明点O₁到平面AB₁C所引垂线的垂足一定在∠AB₁C的平分线B₁O上.设O₁E⊥平面AB₁C，连结OO₁.在Rt△OO₁B₁中，因为O₁E·OB₁＝OO₁·O₁B1，所以

所以A1C1与B1C间的距离为

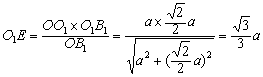
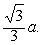
解法2 如图3，容易证明B₁C所在的平面AB₁C与A₁C₁所在的平面A₁D_C1平行.设对角线BD₁与这两个平面的交点分别为E,F.根据三垂线定理和直线与平面垂直的判定定理，可证出BD₁垂直于这两个平面.因而EF即为这两个平行平面间的距离.即为A₁C₁与B₁C间的距离.在Rt△BB₁D₁中，BB₁²＝BE·BD₁，所以

同理

所以

EF=BD1

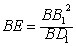
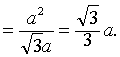
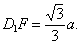
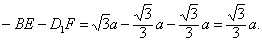
图3

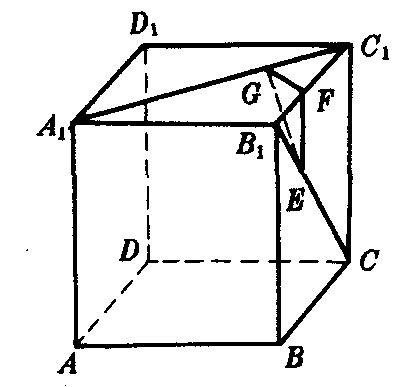
图4

解法3 如图4，在B₁C上任取一点E，在平面BC₁内过E作EF⊥B₁C₁于F，则EF⊥平面A₁C₁.在平面A₁C₁内作FG⊥A₁C₁于G.连结EG.由三垂线定理得EG⊥A₁C₁.所以EG是点E到A1C₁上各点连线中最短者.设EF=x.因为∠EB₁F=45°，所以B₁F=x.C₁F=a-z.

又∠FC1G＝45°，所以

在Rt△EFG

中，

所以EG2的最小值为

因此EG的最小值为

于是A1C1与B1C间的距离为