称量Chengliang
指用称或天平称重量或比较重量。从趣味数学的角度来看,称量问题有二类,一是怎样安排可使称量次数最少,二是一定数目的砝码,最多可以称多少种不同的重量。
例1:有10堆银币,其中有一堆伪币, 已知真币每枚重10克,伪币每枚重9克,请用称称一次,确定哪一堆是伪币。
例2:有五个轻重不同的物件,要求把它们按由轻到重顺序排列起来,有一台没有砝码的天平可供比较任意两个物件的轻重。试问,最少称几次?如何称法?
例3:为能称出从1克至40克所有整数克的重量(用天平),最少需几只砝码,这些砝码各是多少克。
例4:9个小球,其中有一只坏球,已知好球重量都一样,而坏球比好球轻一些,试用无砝码的天平称两次, 找出坏球。
例5: 有12个小球, 其中有一个坏球, 已知好球重量都一样,而坏球与好球的重量不同,但不知轻重,试用天平称3次,挑出坏球,并确定它比好球是轻还是重。
解答:
1.把10堆硬币从1到10编号,从第一堆中取出一枚,第二堆中取出2枚,第三堆中取出3枚, ……,第十堆中取出10枚,共计55枚,一起上称称量,如果都是真银币,总重量应为550克,其中有多少伪币,重量就减少多少克, 由此即可确定伪币的所在。
2. 如果运气好,称4次就可以把5物件按由轻到重的顺序排成一列,称法是,先称两个,碰巧拿到两个最重的,第二次时碰巧又拿到剩下的球中最重的,与上次较轻的一个比较,依次类推,每次都碰巧拿到剩下的球中最重的,但是这种方案在运气不好时,则需称8次以上, 因而不合要求。正确的称量方案如下图示,
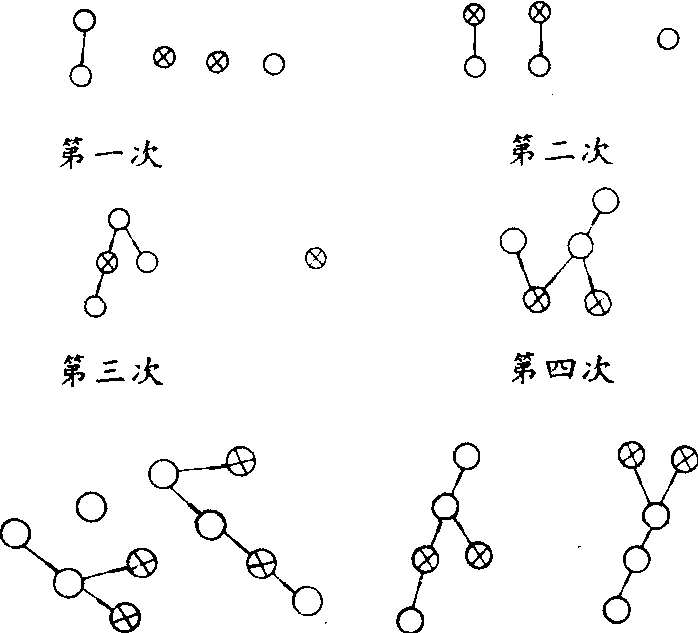
第五次 第六次
各图中的小圈代表物体, 箭头由较重的物件指向较轻物件,带‘×’号的小圈表示下一次要称量的两个物件。
3. 只要1、3、9、27克重的砝码各一个共4个砝码就够了。这一问题可以从以下的思路入手,假定有m个砝码,称量物品时,各砝码均有三种可能位置,放在天平左盘、右盘,或不上天平,m个砝码共有3m种不同放置方式,如果都不放在天平上,那么称不出重量,故此种情形应予排除。其余的可能归中, 由于交换两盘中的砝码, 所称重量不变,故m个砝码最多称出3m-1/2种不同重量,因此要称1至40克的40种不同重量至少需4个砝码, 至于重量确定,1°砝码总重量应为40克,因若超过40克那么据上述,砝码数应不止4个。2°必须有1克的砝码,否则39克的重量无法称量,3°任何二个砝码重量之差大于1克,否则能称量的不同重量少于40种。4°为称37克的重量必须有3克的砝码 (由3°, 没有2克的砝码)。5°与3°的道理相同,其余2个砝码重量均不少于8克, 为称31克, 必须有一9克的砝码。
4. 把9个小球3个一组分成3组,取其中两组放在天平两端,若一样重,则坏球在其余 一组,不一样重则坏球在较轻的一组,这样一次称量,可以把坏球的可能范围缩小到3个,从这三个球中取2个称量,若一样重则其余的一个是坏球,若不一样重,则较轻的一个是坏球。
5.这是六十年代北京市中学生数学竞赛试题,称量办法如下:
把12个球分为3组,每组4个球,取其中两组用天平称量。
情形1°, 两组一样重, 那么坏球在其余4个球之中,从中取3个,另取3个好球(已称过的8个称都是好的)分别放在天平两盘内,若重量不等,用例4的方法即可解决问题。否则,剩下的一个球是坏球,另取一好球与之比较, 即知坏球轻重。
情形2°, 两组重量不等, 那么给轻组的4个球做上标记L1, L2, L3, L4,重组4个球则标以W1,W2,W3, W4。把L1,L2, W1,W2放在天平左盘,L3, W3另加2个好球放在天平右盘,1°若左边轻,则坏球只能在L1,L2, W3中2°,若左边重,则坏球只能在W1,W2,L3之中,3°若一样重,则坏球在L4,W4之中。对于1°、2°, 取L1,L2 (W1,W2)比较,轻(重)者是坏球,若一样重,则W3 (L3)是坏球。对于3°,取一好球与L4比较, 若一样W4是坏球, 不一样, L4是坏球。
例2到例5虽说是初等的称量问题, 但与当代应用数学分支之一——信息论有联系, 如果采用信息论的思想, 问题将变得十分简单。