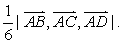向量混合积的几何意义xiangliang hunheji de jibe yiyi

❶当a,b,c成右手系时，0≤(a×b,c)<π/2，因此cos (a×b,c) >0. 以a,b,c为棱作平行六面体 (图1). 由于a×b⊥a，且a×b⊥b，所以| c |·cos (a×b,c)就是此平行六面体的高.根据向量积的几何意义，|a×b|就是以a,b为边的平行四边形面积，从而a×b ·c=|a×b|· |c|cos (a×b,c)=平行六面体的底面积×高=平行六面体的体积.

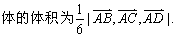
图1

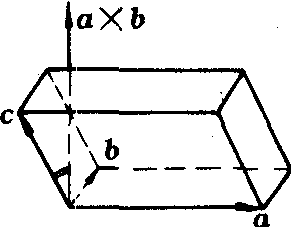
图2

❷ 当a,b,c成左手系时，π/2<(a×b,c)≤π，因此cos (a×b×c) <0，这时|c|·cos 为图2中平行六面体的高的相反数. 从而a×b ·c=|a×b||c|·cos =平行六面体的底面积×高的相反数=平行六面体的体积的相反数.
由以上分析，可知向量混合积的几何意义是：❶ 向量a,b,c共面的充要条件是 =0.

❷ 以不共面向量a,b,c为棱的平行六面体体积为|a,b,c|.

❸ 以空间不共面四点A,B,C,D为顶点的四面体的体积为