复数的乘法fushu de chengfa
按照多项式乘法法则进行,并在结果中将i2写成-1,把实部与虚部分别合并.即
(a+bi)(c+di)=ac+bci+adi+bdi2
=(ac-bd)+(bc+ad)i
这就是复数的乘法法则.
显见,任意两个复数的积仍是一个复数.其中,两个共轭复数的积是一个实数,它等于其中每一个复数的模的平方.即
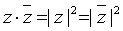
容易验证复数乘法满足交换律与结合律,乘法对加法满足分配律.即对于任何复数z1,z2,z3.有
| z1·z2=z2·z1, |
| (z1·z2)·z3=z1·(z2·z3), |
| z1(z2+z3)=z1·z2+z1·z3. |
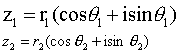
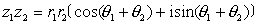
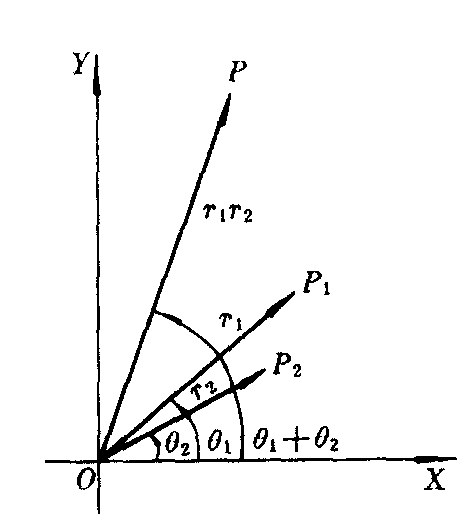
图1
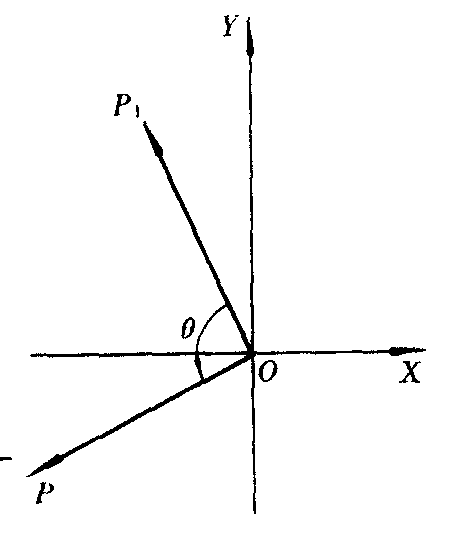
图2
由这个法则易得到复数乘法的几何意义:把复数z1对应的向量
 按逆时针方向旋转角θ2(若θ2<0,则按顺时针方向旋转角|θ2|),并把它的模变为原来的r2倍所得向量
按逆时针方向旋转角θ2(若θ2<0,则按顺时针方向旋转角|θ2|),并把它的模变为原来的r2倍所得向量 就是复数z1=r1(cosθ1+isinθ1)与z2=r2(cosθ2+isinθ2)的积z1z2所对应的向量(图1).若将复数z1所对应的向量
就是复数z1=r1(cosθ1+isinθ1)与z2=r2(cosθ2+isinθ2)的积z1z2所对应的向量(图1).若将复数z1所对应的向量 按逆时针方向旋转角θ所得向量
按逆时针方向旋转角θ所得向量 图2),便是复数z1与模为1幅角为θ的复数之积所对应的向量.例如,将复数1 +i所对应向量OP1按逆时针方向旋转120°所得向量
图2),便是复数z1与模为1幅角为θ的复数之积所对应的向量.例如,将复数1 +i所对应向量OP1按逆时针方向旋转120°所得向量 所对应的复数便是
所对应的复数便是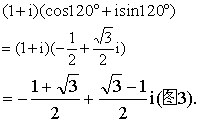
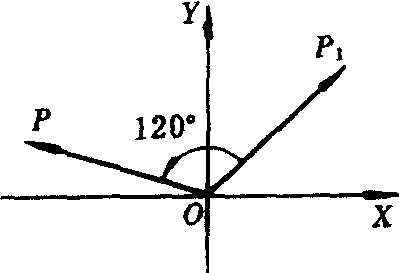
图3
用数学归纳法容易证明n个复数相乘时,积的模等于各个复数模的积,积的幅角等于各个幅角之和. 即
若 zi=ri(cosθi+isinθi) (i=1,2,…,n)则z1·z2·…·zR= r1·r2·…·rR[cos(θ1+θ2 + …+ θn) + isin(θ1 + θ2 +…+ θn)].