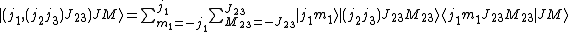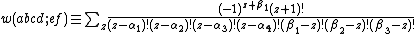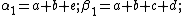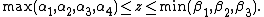- Recoupling coefficients
- Algebra
- Relation to Wigner's 6-j symbol
- See also
- Notes
- Further reading
- External links
Racah's W-coefficients were introduced by Giulio Racah in 1942.[1] These coefficients have a purely mathematical definition. In physics they are used in calculations involving the quantum mechanical description of angular momentum, for example in atomic theory.
The coefficients appear when there are three sources of angular momentum in the problem. For example, consider an atom with one electron in an s orbital and one electron in a p orbital. Each electron has electron spin angular momentum and in addition
the p orbital has orbital angular momentum (an s orbital has zero orbital angular momentum). The atom may be described by LS coupling or by jj coupling as explained in the article on angular momentum coupling. The transformation between the wave functions that correspond to these two couplings involves a Racah W-coefficient.
Apart from a phase factor, Racah's W-coefficients are equal to Wigner's 6-j symbols, so any equation involving Racah's W-coefficients may be rewritten using 6-j symbols. This is often advantageous because the symmetry properties of 6-j symbols are easier to remember.
Racah coefficients are related to recoupling coefficients by
Recoupling coefficients are elements of a unitary transformation and their definition is given in the next section. Racah coefficients have more convenient symmetry properties than the recoupling coefficients (but less convenient than the 6-j symbols).[2]
Recoupling coefficients
Coupling of two angular momenta  and
and 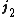 is the construction of simultaneous eigenfunctions of
is the construction of simultaneous eigenfunctions of  and
and  , where
, where  , as explained in the article on Clebsch–Gordan coefficients. The result is
, as explained in the article on Clebsch–Gordan coefficients. The result is
where  and
and  .
.
Coupling of three angular momenta  ,
, 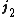 , and
, and  , may be done by first coupling
, may be done by first coupling  and
and 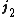 to
to  and next coupling
and next coupling  and
and  to total angular momentum
to total angular momentum  :
:
Alternatively, one may first couple 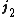 and
and  to
to  and next couple
and next couple  and
and  to
to  :
:
Both coupling schemes result in complete orthonormal bases for the  dimensional space spanned by
dimensional space spanned by
Hence, the two total angular momentum bases are related by a unitary transformation. The matrix elements of this unitary transformation are given by a scalar product and are known as recoupling coefficients. The coefficients are independent of  and so we have
and so we have
The independence of  follows readily by writing this equation for
follows readily by writing this equation for 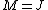 and applying the lowering operator
and applying the lowering operator  to both sides of the equation.
to both sides of the equation.
Algebra
Let
be the usual triangular factor, then the Racah coefficient is a product
of four of these by a sum over factorials,
where
and
The sum over  is finite over the range[3]
is finite over the range[3]
Relation to Wigner's 6-j symbol
Racah's W-coefficients are related to Wigner's 6-j symbols, which have even more convenient symmetry properties
Cf.[4] or
See also
- Clebsch–Gordan coefficients
- 3-jm symbol
- 6-j symbol
- Pandya theorem
Notes
2. ^Rose, M. E. (1957). Elementary theory of angular momentum (Dover).
3. ^Cowan, R D (1981). The theory of atomic structure and spectra (Univ of California Press), p. 148.
4. ^Brink, D M & Satchler, G R (1968). Angular Momentum (Oxford University Press) 3
 ed., p. 142. [https://archive.org/details/AngularMomentum online]
ed., p. 142. [https://archive.org/details/AngularMomentum online]Further reading
- {{cite book |last= Edmonds |first= A. R. |title= Angular Momentum in Quantum Mechanics |year= 1957
|publisher= Princeton University Press |location= Princeton, New Jersey |isbn= 0-691-07912-9}}
- {{cite book |last= Condon |first= Edward U. |author2=Shortley, G. H. |title= The Theory of Atomic Spectra |year= 1970
|publisher= Cambridge University Press |location= Cambridge |isbn= 0-521-09209-4 |chapter= Chapter 3}}
- {{cite book |last= Messiah |first= Albert |title= Quantum Mechanics (Volume II) |year= 1981 | edition= 12th
|publisher= North Holland Publishing |location= New York |isbn= 0-7204-0045-7}}
- {{cite journal
|first=Masachiyo
|last1=Sato
|journal=Progr. Theor. Physics
|volume=13
|issue=4
|year=1955
|pages=405–414
|title=General formula of the Racah coefficient
|doi=10.1143/PTP.13.405
|bibcode=1955PThPh..13..405S
}}
- {{cite book |last= Brink |first= D. M. |author2=Satchler, G. R. |title= Angular Momentum
|year= 1993 |edition= 3rd |publisher= Clarendon Press |location= Oxford |isbn= 0-19-851759-9 |chapter= Chapter 2 }}
- {{cite book |last= Zare |first= Richard N. |title= Angular Momentum |year=1988
|publisher= John Wiley |location= New York |isbn= 0-471-85892-7 |chapter= Chapter 2}}
- {{cite book |last= Biedenharn |first= L. C. |author2=Louck, J. D. |title= Angular Momentum in Quantum Physics
|year= 1981 |publisher= Addison-Wesley |location= Reading, Massachusetts |isbn= 0-201-13507-8 }}
External links
- {{springer|title=Racah-Wigner coefficients|id=p/r110010}}
- Humic substance
- Humid
- Humid Chaco
- Humid continental climate
- Humidex
- Humidifier
- Humidifiers
- Humidity
- Humidor
- Humid Pampas/version 2
- Humid Teenage Mediocrity 1992–1996
- Humiliate
- Humiliated
- Humiliated and Insulted
- Humiliati
- Humiliating
- Humiliation
- Humiliation (BDSM)
- Humiliator
- Humiliatrix
- Humility
- Humin
- Humint
- Humira
- Humite