匹配pipei

一个图中互不邻接的边的集合.设图G=〈V,E〉若M⊆E，且M中任二边均无公共端点（不邻接），则称M是G的一个匹配（也称为边无关集或对集）;M的边的端点称为(G关于M的)M-饱和点，G的其它点称为M-非饱合点.例如图，有M={e₂,e₄,e₈},M₁＝{e₃,e₇},M₂＝{e₁,e₇}都是G的匹配.而M-饱和点是v₁,v₃,v₂,v₄,v₅,v₆;M₁-饱和点为v₂、v₃、v₄、v₅;M₂-饱和点为v₁、v₂、v₄、v₅.

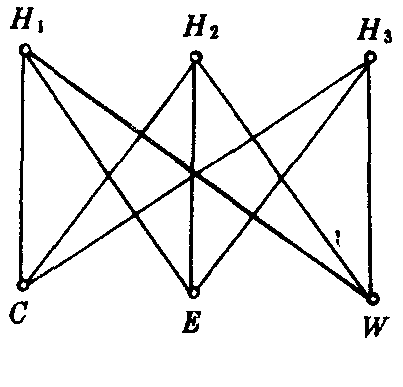
K_3.3

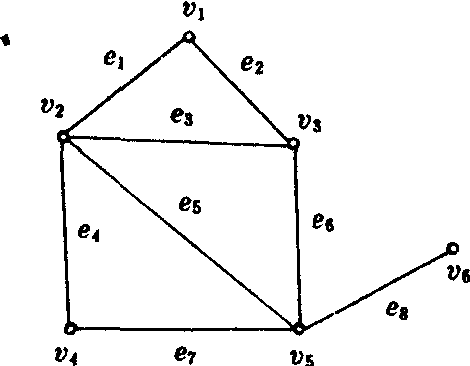
若G的所有点都是(匹配M的) M-饱和点，则称M是G的一个完美匹配（完美边无关集）.若G有完美匹配，则G必有偶数个点.显然逆命题不一定成立.
上面图G中，M是一个完美匹配.而M₁,M₂都不是完美匹配.而下图G₁没有完美匹配.

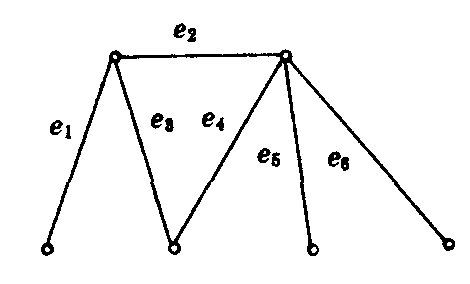
G₁

若M是G的匹配，并且不存在匹配M′，使|M′|>|M|，则称M是G的最大匹配.
G的完美匹配是G的最大匹配.其逆不真.
上图G₁,{e₁,e₄,},{e₃,e₅},{e₃,e₆}都是G₁的最大匹配，而G₁没有完美匹配.
若G=〈V₁,V₂;E〉是二分图，V₁＝{v₁,v₂，…，v_p},V₁对V₂的匹配指的是G的子图，边为v₁u₁,v₂u₂，…，v_pu_p是G的边，且u₁,u₂，…，u_p是V₂中不同的点.

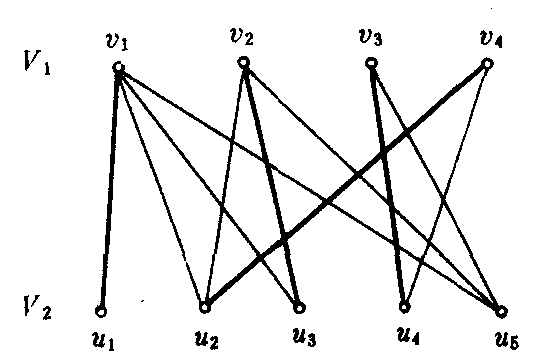
G

例如图，其中的粗线表示的是G中V₁对V₂的一个匹配.
许多实际问题可化为在二分图中求匹配的问题.有m个工作人员及n件工作的单位，每个人只熟悉其中若干件工作，而每件工作都需要一个人去干.能否将这n件工作分配给熟悉它的人去干？用V₁＝{v₁,v₂，…，v_m},V₂＝{u₁,u₂，…，u_n}表示人与工作的集合，v_i熟悉工作u_j，则v_iu_j为边.则得到二分图.于是问题化为：能否在这个二分图中，找出V₁对V₂的匹配.
定理：设G=〈V₁,V₂;E〉.G中存在V₁对V₂的匹配，当且仅当V₁中任意k点(k=1,2，…|V₁|)至少和V₂中k个点相邻接（该条件称为相异性条件）.
定理：设G=〈V₁,V₂;E〉.若存在正整数t，并且：
❶对V₁中每个点，至少有t条边(即度数≥t);
❷对V₂中每个点，至多有t条边(即度数≤t)；则G具有V₁对V₂的匹配.例如二分图G

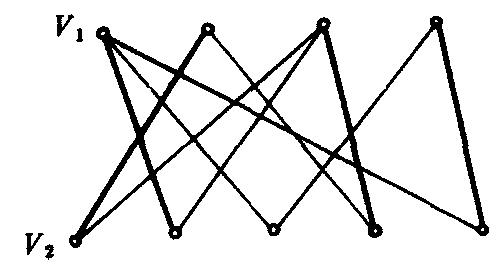
G

t=2，对V₁的每个点v，适合d(v)≥2，而对于V₂的每个点u,d(u)=2.存在V₁对V₂的匹配（粗线表示的就是一个）.