- Quantitative consideration
- Application
- See also
- References
Ehrenfest equations (named after Paul Ehrenfest) are equations which describe changes in specific heat capacity and derivatives of specific volume in second-order phase transitions. The Clausius–Clapeyron relation does not make sense for second-order phase transitions,[1] as both specific entropy and specific volume do not change in second-order phase transitions.
Quantitative consideration
Ehrenfest equations are the consequence of continuity of specific entropy 
and specific volume 
, which are first derivatives of specific Gibbs free energy – in second-order phase transitions. If one considers specific entropy as a function of temperature and pressure, then its differential is:
.
As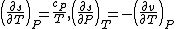 
, then the differential of specific entropy also is:
,
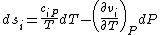where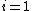 
and 
are the two phases which transit one into other. Due to continuity of specific entropy, the following holds in second-order phase transitions: 
. So,
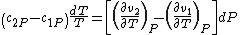
Therefore, the first Ehrenfest equation is:
.
The second Ehrenfest equation is got in a like manner, but specific entropy is considered as a function of temperature and specific volume:
The third Ehrenfest equation is got in a like manner, but specific entropy is considered as a function of and 
:
.
Continuity of specific volume as a function of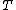 
and gives the fourth Ehrenfest equation:
.
Application
Derivatives of Gibbs free energy are not always finite. Transitions between different magnetic states of metals can't be described by Ehrenfest equations.
See also
- Paul Ehrenfest
- Clausius–Clapeyron relation
- Phase transition
References
- Ibn Ishaq
- Ibn Janach
- Ibn Jubayr
- Ibn Juzayy
- Ibn Kather
- Ibn Kathir
- Ibn Khaldon
- Ibn Khaldoun
- Ibn Khaldun
- Ibn Khaldūn
- Ibn Khallikan
- Ibn Khaseb
- Ibn Khordadbeh
- Ibn Madja
- Ibn Maga
- Ibn Majah
- Ibn Majeh
- Ibn Masarrah
- Ibn Nafis
- Ibn Paquda Bahya
- Ibn Qayyim
- Ibn Qayyim al-Jawziyya
- Ibn Qudama
- Ibn Qudamah
- Ibn Qutaiba