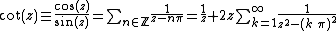1. Theorem

2. Example

3. Pole expansions of meromorphic functions

4. See also

5. References

6. External links

In complex analysis, Mittag-Leffler's theorem concerns the existence of meromorphic functions with prescribed poles. Conversely, it can be used to express any meromorphic function as a sum of partial fractions. It is sister to the Weierstrass factorization theorem, which asserts existence of holomorphic functions with prescribed zeros. It is named after Gösta Mittag-Leffler.

Theorem

Let be an open set in and a closed discrete subset. For each in , let be a polynomial in . There is a meromorphic function on such that for each , the function has only a removable singularity at . In particular, the principal part of at is .

One possible proof outline is as follows. Notice that if is finite, it suffices to take . If is not finite, consider the finite sum where is a finite subset of . While the may not converge as F approaches E, one may subtract well-chosen rational functions with poles outside of D (provided by Runge's theorem) without changing the principal parts of the and in such a way that convergence is guaranteed.

Example

Suppose that we desire a meromorphic function with simple poles of residue 1 at all positive integers. With notation as above, letting

and , Mittag-Leffler's theorem asserts (non-constructively) the existence of a meromorphic function with principal part at for each positive integer . This has the desired properties. More constructively we can let

.

This series converges normally on (as can be shown using the M-test) to a meromorphic function with the desired properties.

Pole expansions of meromorphic functions

Here are some examples of pole expansions of meromorphic functions:

See also

• Riemann-Roch theorem
• Weierstrass factorization theorem
• Liouville's theorem
• Mittag-Leffler condition of an inverse limit

References

• {{citation|first=Lars|last=Ahlfors|authorlink=Lars Ahlfors|title=Complex analysis|publisher=McGraw Hill|year=1953|publication-date=1979|edition=3rd|isbn=0-07-000657-1}}.
• {{citation|first=John B.|last=Conway|title=Functions of One Complex Variable I|publisher=Springer-Verlag|year=1978|publication-date=1978|edition=2nd|isbn=0-387-90328-3}}.

External links

• {{springer|title=Mittag-Leffler theorem|id=p/m064170}}
• {{planetmath reference|title=Mittag-Leffler's theorem|id=3732}}

• IgA nephropathy
• Iganga District
• Iga Province
• Iga province
• Igara
• Igaram
• Igarapava
• Igaratá
• Igaraçu do Tietê
• Igarka
• IGA Stadium
• IGA (supermarkets)
• IGATE Patni
• Igatpuri
• I. G. Baker
• I. G. Baker Company
• Igbaras
• Igbira
• Igbirra
• Igbo (ethnic group)
• Igboid
• Igboid languages
• Igbo language
• Igbo legends
• Igbo myth