二次函数及图象erci hanshu ji tuxiang

形如y=ax²+bx+c(其中a,b,c均为常数，a≠0)的函数，叫做二次函数.它的定义域是实数集R.当a>0时，它在区间(-∞,-b/2a〕是单调减的，在区间〔-b/2a,+∞)是单调增的；x=-b/2a时，它有极小值（最小值） (4ac-b²)/4a；当a<0时，它在区间(-∞,-b/2a〕是单调增的，在区间〔-b/2a,+∞)是单调减的，x=-b/2a时，它有极大值（最大值）(4ac-b²)/4a.
例如：函数y=2x²-3是二次函数，它在区间(-∞,0〕是单调减的，在区间〔0,+∞)是单调增的，x=0时，它有极小值-3.函数y=-(1/3) x²+2x+1也是二次函数，它在区间(-∞,+3〕是单调增的，在区间〔+3,+∞)是单调减的，x=3时，它有极大值4.
二次函数y=ax²+bx+c(a≠0)变形为y=a(x+b/2a)²+ (4ac-b²)/4a.其图象是一条抛物线，顶点为(-b/2a,(4ac-b²)/4a)，对称轴方程为x=-b/2a.抛物线的开口的方向及大小由a来决定.当a>0时，抛物线的开口向上；当a<0时，抛物线的开口向下.当|a|越大时，抛物线开口越小；当|a|越小时，抛物线的开口越大.
例如：二次函数y=2x²-3的图象的顶点为(0,-3)，对称轴方程为x=0，开口向上.二次函数y=-(1/3) x²+2x+1=-(1/3)(x-3)²+4的图象的顶点为(3,4)，对称轴方程为x=3，开口向下，比前一条抛物线的开口要大.它们的图象分别如图1、图2所示.

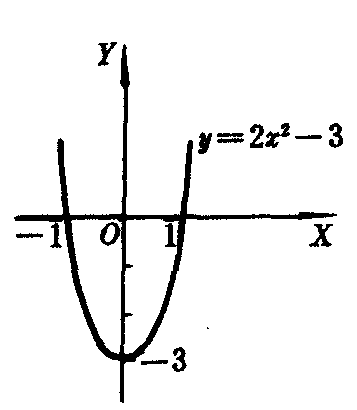
图1

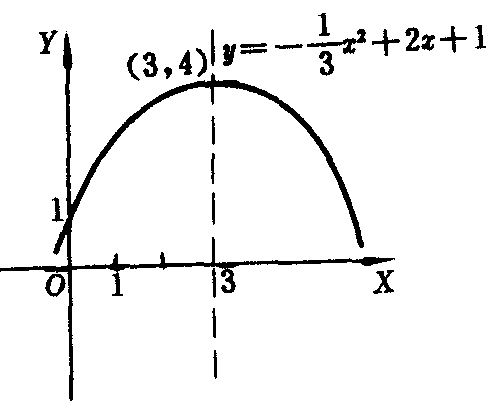
图2

二次函数y=ax²+bx+c (a≠0)与一元二次方程ax²+bx+c=0(a≠0)及一元二次不等式ax²+bx+c>0或ax²+bx+c<0 (a≠0)有着密切的联系.例如，二次函数y=ax²+bx+c的图象抛物线与X轴的交点的横坐标就是一元二次方程ax²+bx+c=0的根.反之，若方程ax²+bx+c=0有两个不等实根，则抛物线y=ax²+bx+c与X轴有两个交点；若方程ax²+bx+c=0有两个相等实根，则抛物线y=ax²+bx+c与X轴只有一个交点；若方程ax²+bx+c=0没有实根，则抛物线y=ax²+bx+c与X轴没有交点.利用二次函数的图象可以更直观地理解一元二次不等式的解集.对于一元二次不等式ax²+bx+c>0 (a>0)，设△=b²-4ac.如果△>0，方程ax²+bx+c=0有两相异实根x1,x₂ (x₁2)，抛物线y=ax²+bx+c与X轴有两个交点(如图3)，那么，不等式ax²+bx+c>0的解集是x1或x>x₂.而不等式ax²+bx+c<0的解集是x₁2;

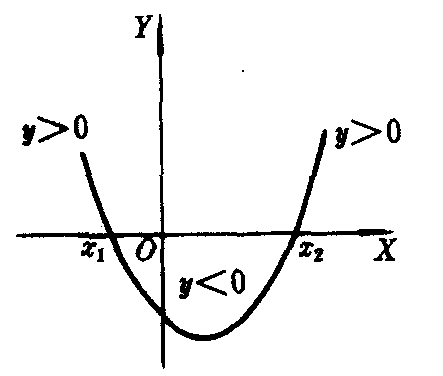
图3

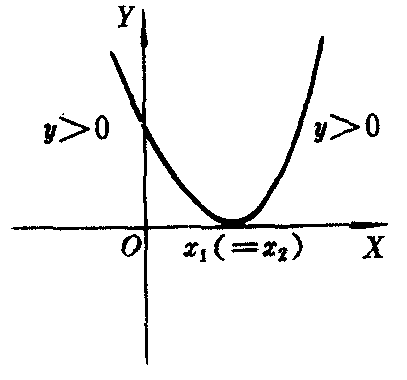
图4

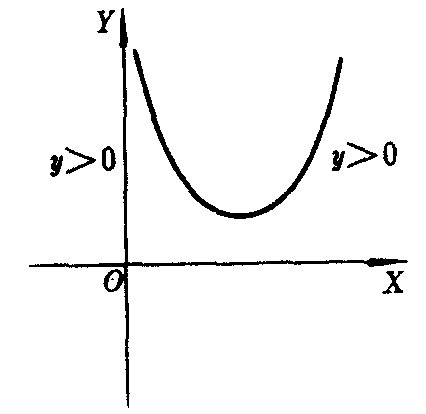
图5

如果△=0，方程ax²+bx+c=0有两个相等实根x₁＝x₂＝-b/2a，抛物线y=ax²+bx+c与X轴只有一个交点(如图4)，那么，不等式ax²+bx+c>0的解集是所有不等于-b/2a的实数.而不等式ax²+bx+c<0的解集是空集；如果△<0，方程ax²+bx+c=0无实根，抛物线y=ax²+bx+c与X轴没有交点(如图5)，那么，不等式ax²+bx+c>0的解集是全体实数.而不等式ax²+bx+c<0的解集是空集.