计数问题Jishu wenti

计数就是数数，就是要确定某一给定集合中元素的个数。例如，在同一直线上有5个不同点， 问以这5个给定点为端点的线段共有多少条。象这样的问题如果采用“笨数”的办法，只要记清楚哪条数过哪条没数过是能够数清的。但是这样做既麻烦又容易出错。因此应该启发学生去观察思考，寻找出简便可靠的巧妙办法来解决问题。对于上例，可以从两个点的情况出发，逐次加点，寻找规律。只有两个点的情况，显然只有1条线段，若再添加一点，则新点与原来的每一点均构成一线段， 于是线段数增加了两条变成3条。循着这条思路，很容易算出：在5个点的情形下，共有10条不同线段。进一步的思考，不难得到更深刻的结论，假如直线上已有几个点，再添加一个新点则线段数目将增加几条，（新点与每一原有点均构成一新线段）于是可以得到一般情况下的计算公式，设直线上给定n+1个点，则线段数目为1+2+3+…条。式中的等号为什么成立请参阅“数列的求和”条。再看一个例子(图1), 请数出图中正方形的个数， 图中的正方形有大有小， 互相交迭， 用笨数的办法很难数清， 由于形状不太规则好的计数方法不容易直接求得， 因此解决这一问题需要采用迂回战术， 先看下面较为简单的问题： 计算图2中正方形的个数。显而易见，图中正方形的总数等于边长为1的正方形总数加上边长为2的正方形总数再加上边长为3的及边长为4的正方形总数。不难看出这四个数分别是4×7,3×6,2×5,1×4, 因而图中正方形总数为4×7+3×6+2×5+1×4=60。由此可以推算出更一般的结果： 假定有m×n的方格子图形， m≤n, 则其中的正方形个数为m×n+ (m-1) × (n-1) +…+1×
(n-m+1)。与图2相比，图1缺少四角，因而计数时占据角部的正方形不应计算在内， 这种正方形中边长为1、2、3的各有4个，因为4已是整个图形的宽，故边长为4而占据角部的正方形只有2个，因此，图1中正方形个数比图2中的要少4+4+4+2=14个，于是得出图1中正方形个数是46。再看一个更复杂一点的图形 (图3)。
我们已经算出图1中正方形个数为46个。根据同样的想法不难求出图3中正方形个数为6×5+5×4+4×3+3×2+2×1-4×4-2=52。而图4可以看作图1与图3的迭合， 故图4中正方形个数是52+46-40=58个， 其中40是图3与图4两图形重合部分 (5×4方格图形) 中正方形的个数。

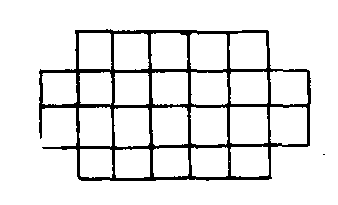
图1

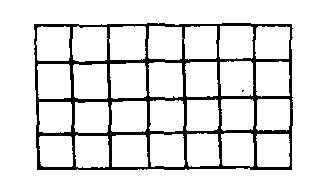
图2

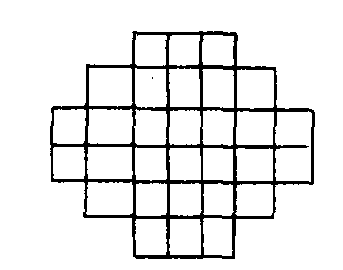
图3

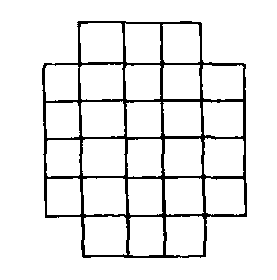
图4